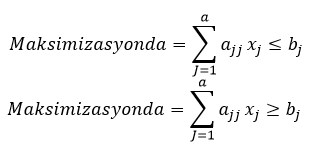Kereste Endüstrisinde Kullanılan Optimizasyon Yöntemleri

Doç. Dr. Süleyman KORKUT
Düzce Üniversitesi, Orman Fakültesi
suleymankorkut@hotmail.com

Mital’a (1987) göre optimizasyon, bir matematiksel fonksiyonun en büyük (maksimum) ya da genellikle en küçük (minimum) değerlerini belirleme işlemidir. Optimizasyon problemi c(x) ≤ 0 ve h(x)=0 kısıtlamaları altında U=U(x) skaler fonksiyonunun değerini en aza indirgeme problemidir. c(x) ve h(x), genelde x’in doğrusal olmayan vektör değerli fonksiyonlarıdır. Kabul edilebilirlik bölgesi; R_A={x|c(x) ≤0, h(x)=0}biçiminde tanımlanır. R_A bölgesine ait herhangi bir nokta kabul edilebilir bir noktadır.  Amaç fonksiyonu maliyet fonksiyonu ya da hata fonksiyonu olarak da adlandırılır. Optimizasyon işleminin amacı R_A bölgesinde her x ε R_A için U(x*)≤U(x) olacak biçimde x* değerini belirlemektir.  Burada x*, U(x)’in global minimumudur [1].

Genel olarak optimizasyon, bir fiziksel sistemi gerçekleştirmede en uygun çözümü elde etme yöntemidir.  Matematiksel optimizasyonun bir çok mühendislik alanında kullanılması sonucu bir çok optimizasyon yöntemi ortaya çıkmıştır. Optimizasyon yöntemlerinin genel bir sınıflandırması aşağıda verilmiştir.  Kısıtlanmamış fonksiyonlar için verilen optimizasyon yöntemleri; hiçbir yan koşul veya yan kısıt olmaksızın verilen bir f(x) yada f(x₁,…..,x_n) fonksiyonunun optimum (minimum yada maksimum) noktasının bulunmasında kullanılır. Kısıtlanmış fonksiyonlar için optimizasyon yöntemleri; bazı eşitlik ve/veya eşitsizlik kısıtlarına bağlı olarak verilen bir f(x) yada f(x₁,…..,x_n) fonksiyonunun optimum noktasını bulmak için kullanılırlar. Sistem ya da bilgi akış yapısı kullanan yöntemlerine ise dinamik programlama örnek olarak verilebilir [2].

Optimizasyon yöntemlerinin sınıflandırılması [2];

1. Bir değişkenli kısıtlanmış fonksiyonlar için optimizasyon yöntemleri
2. Analiz yöntemleri
3. Birinci türev için sayısal kök bulan yöntemler
   • Newton yöntemi
   • Yanlış konum yöntemi
   • Yarı aralık yöntemi
   • Polinom yöntemleri
4. Arama yöntemleri

c1- Eş zamanlı yöntemler

• Ayrıntılı arama
• Rasgele arama

      c2- Sıralı yöntemler

• Dichotomous arama
• Eşit aralıklı arama
• Altın oran ile arama
• Fibonacci arama

2. Çok değişkenli kısıtlanmamış fonksiyonlar için optimizasyon yöntemleri

1. Analiz yöntemleri
2. Birinci türev için sayısal kök bulan yöntemler

– Newton-Raphson yöntemi

1. Fonksiyon değerini kullanan arama yöntemleri

c1- Eş zamanlı yöntemler

• Ayrıntılı arama
• Rasgele arama

      c2- Sıralı yöntemler

• Üstel rasgele arama
• Kafes arama
• Tek değişkenli arama
• Dönen koordinat yöntemi
• Doğrudan arama

1. Fonksiyon ve birinci türev değerini kullanan arama yöntemleri

– Kontur teğet yöntemi
– Steepest descent yöntemleri
– Patran yöntemleri
– Gradyen eşleniği yöntemleri

1. Fonksiyon, birinci ve ikinci türev değerlerini kullanan arama yöntemleri

– Steepest descent yöntemleri
– Gradyen eşleniği yöntemleri

3. Kısıtlanmış fonksiyonlar için optimizasyon yöntemleri
4. Lineer programlama
5. Nonlineer programlama

– Varyasyonel hesap: Lagrange çarpanları yöntemi
– Kuadratik programlama
– Genel nonlineer problemler

4. Sistem ya da bilgi akış yapısını kullanan optimizasyon yöntemleri

Dinamik programlama

Bu tanımlardan hareketle optimizasyon terimini kereste endüstrisine adapte edecek olursak kereste üretiminde çıktıların girdilere oranının, sadece biçme işlemi düşünülürse kereste hacminin tomruk hacmine oranının bir başka deyişle randımanın maksimize edilmesi optimizasyon olarak tanımlanabilir [3].

Kereste endüstrisinde ister tüm üretim, ister sadece biçme ele alınsın en fazla kullanılan optimizasyon yöntemi doğrusal programlama yöntemidir.  Doğrusal programlama, verilen doğrusal eşitsizliklere diğer bir deyimle kısıtlara bağlı olarak verilen doğrusal amaç fonksiyonunu maksimum (minimum) yapan negatif olmayan gerçek değerlerin seçilmesi olarak tanımlanabilir [4].  Köse vd. (2000)’e göre doğrusal programlama; saptanmış bir amacı gerçekleştirmek için kısıtlı kaynakların etkin kullanımını ve çeşitli seçenekler arasında en uygun dağılımını sağlayan matematiksel bir yöntemdir. Bir başka deyişle işletme sorunlarında yer alan para, malzeme, makine, zaman, insan gücü, donanım vb. kaynakların çeşitli kısıtlayıcı koşullar altında en iyi yararı sağlayacak şekilde birleştirilmesini sağlayan yöntemdir [5].

Doğrusal kelimesi ile bütün fonksiyonların doğrusal olması, programlama kelimesi ile de bir hareket planının seçilmesi yani optimum (en uygun) kararın alınması ifade edilmektedir. Matematiksel açıdan, doğrusal programlama modeli; amaç fonksiyonu ve sınırları doğrusal olan bir sınırlı optimizasyon problemidir. Doğrusal programlama problemi adı verilen bu sınırlı optimizasyon probleminde amaç fonksiyonu maksimize edilmesi halinde; üretim, kâr katkısı gibi büyüklükleri ifade eder. Eğer amaç fonksiyonu minimize edilirse; maliyet, artık, boş zaman gibi büyüklükleri ifade eder. Sınırlar ise genellikle iş gücü, depo alanı ve işletme sermayesi gibi kıt kaynakları gösterir [6].

Bir DP (Doğrusal Programlama) uygulamasının ilk ve en önemli aşaması ele alınan karar probleminin bir DP problemi haline getirilmesi yani başka bir deyişle DP probleminin formüle edilmesidir [6].

Bir karar problemine çözüm getirebilmek için her şeyden önce ulaşılmak istenen amaç, açık ve seçik olarak ortaya konulmalıdır. Karar değişkenleri tanımlanırken, bu değişkenlerin kontrol edilebilir olmaları ve aldıkları değerlerin belirli bir dağıtım planını ifade etmeleri zorunluluğu göz önünde bulundurulmalıdır. DP modelinin başarılı bir şekilde uygulanması, sınırların konmasında gösterilen ustalığa büyük ölçüde bağlıdır.  Fiziki, teknik, yasal ve kurumsal nitelikteki sınırların yanında, kişisel ya da subjektif nitelikteki sınırlar da DP modelinde önemli bir yere sahiptirler. Doğrusal programlama probleminin genel matematiksel tanımı aşağıdaki şekildedir [6].

Pozitif kısıtlayıcılar x_j≥0
x_j = Karar değişkenleri
a_ij ve b_i = Sabit olarak verilen değerler
n= Karar değişkeni sayısı

İlter (1998) [7] doğrusal programlamanın, doğrusal bir amaç fonksiyonunun belirli eşitlik veya eşitsizlik şeklinde kısıtlayıcı şartlar altında optimum çözümün elde edilmesi amacıyla kullanıldığını ifade etmiştir.

Doğrusal programlama problemlerinin çözümü amacıyla 1947 yılında George B. Dantzig ve arkadaşları tarafından geliştirilen Simpleks Yöntemi uygulamada en fazla kullanılan yöntemdir. Simpleks yöntemi, özde tablolara dayalı olan aşamalı bir çözüm yöntemi olup, amaç fonksiyonunu ve kısıtları birlikte dikkate almaktadır [4, 5, 6].

Kereste endüstrisinde yöneylem araştırmalarının kullanımı 1970’erden itibaren artmıştır. Yöneylem araştırması (Operations Research), organizasyon sistemlerinin operasyonlarını düzenlemek üzere, karar verme olayına bilimsel bir yaklaşım olarak tanımlanabilir. Yöneylem araştırması, kısaca operasyonlar üzerinde araştırmadır. Yöneylem araştırması, bir organizasyon içindeki operasyonların veya aktivitelerin nasıl koordine edileceği ve nasıl yönlendirileceği problemini çözüme ulaştırmaktadır.  Yöneylem araştırmasının amacı; insan-makine sistemlerinin yapısını, davranışlarını incelemek ve açıklamak, bu sistemlerin amaç ve hedeflerine uygun yönetim ve kontrollerine ilişkin karar verme sorunlarını çözmek ya da bunun için yöntem ve teknikler geliştirmektir [5].

Kereste üretim optimizasyonunda en fazla kullanılan yöneylem araştırma teknikleri aşağıda verilmiştir:

Monte-Carlo Tekniği: Belli bir olaya ilişkin temel bilgilerden yararlanarak rassal örnekleme yöntemini kullanıp olayın yapay olarak ortaya çıkmasını sağlayan bir teknik olarak görülmektedir [7].

Kuyruk Teorisi: Servis olanaklarının optimal sayısının saptanması ve optimal giriş (veya çıkış) sürelerinin ayrı ayrı veya aynı süreçte belirlenmesini incelemektedir [7].

Markov Tekniği: İşletmelerde özellikle pazarlama sorunlarında yaygın olarak kullanılmaktadır [7].

Simülasyon: Simülasyon tekniği, gerçek durumun bir modelini ortaya çıkarıp, bu modelin kullanılmasıyla gerçek durum hakkında sonuçlar elde ederek probleme çözüm aramaktadır. Bir başka deyişle simülasyon modelleri, bir sistemin bileşenleri arasındaki ilişkileri inceleyerek, sistemden sonuç elde etmek amacıyla düzenlenmektedir.  Simülasyon, gerçek bir sistemin modelini tasarlama, kurulan modeli deneme ve değişik stratejiler geliştirme süreci olarak tanımlanmaktadır. Simülasyon istatistiksel bir deney olarak görülmelidir. Sistemin bileşenleri arasındaki etkileşimlerin formüle edilmesiyle, sanki gerçek sistem inceleniyormuş gibi, geliştirilen simülasyon modeli yardımıyla modelde üretilen belirli değişkenlere karşı gerçek sistemin nasıl bir tepki göstereceği tahmin edilebilmektedir.  Simülasyon genellikle matematiksel modellerle ifade edilemeyen karmaşık sistemlerin analizinde esnek bir model olması sebebiyle tercih edilmektedir [5].

Etkin bir simülasyonda, planlama ve organizasyonun büyük bir titizlikle sağlanması gerekir. Simülasyonda izlenecek aşamalar sistemin yapısına ve karmaşıklığına bağlı olarak değişmesine karşın, tüm simülasyon modellerinde uygulanması gereken temel aşamalar bulunmaktadır.  Bu aşamalar sırasıyla aşağıda verilmiştir [5].

– Simüle edilmek istenen sistem ya da problemin tanımlanması
– Kullanılmak istenen modelin formüle edilmesi
– Modelin kontrol edilmesi, diğer bir anlatımla modelin davranışları ile gerçek problemin bulunduğu ortama ilişkin davranış ve sonuçların karşılaştırılması
– Modeli çalıştırmak için gerekli olan verilerin tanımlanması ve toplanması
– Modelin çalıştırılması
– Simülasyon modeli sonuçlarının analiz edilmesi ve eğer arzu ediliyorsa daha farklı çözüm yollarının araştırılması
– Yeni çözüm yollarının araştırılması durumunda simülasyon modelinin yeniden çalıştırılması
– Simülasyon modelinin geçerli olup olmadığının test edilmesi.

---

5846 sayılı yasa gereği lütfen gerektiği gibi kaynak göstermeden alıntı yapmayınız.!

Kaynaklar

1. MITAL, K.V. 1987: Optimization Methods in Operations Research and System Analysis, Wiley Eastern Limited.
2. BUNDAY, B.D. 1984: Basic Optimization Methods, Edward Arnold Pty. Ltd.
3. KORKUT, S. 2003: Kereste Üretiminde Optimizasyon Üzerine Araştırmalar, İ.Ü. Fen Bilimleri Enstitüsü, Basılmamış Doktora Tezi.
4. TÜLÜCÜ, K. 1997: Optimizasyon (Doğrusal Programlama), Ç.Ü. Ziraat Fakültesi Genel Yayın No: 189, Adana.
5. KÖSE, S.; YAVUZ, H.; GÜL, A.U. 2000: Yöneylem Araştırması ve Ormancılık Uygulamaları, K.T.Ü. Orman Fakültesi, Ders Teksirleri Serisi No:61, Trabzon.
6. GÜRAY, A.; USTA, İ. 1993: Mobilya Endüstrisinde “Optimizasyon”, H.Ü. Mesleki Teknoloji Yüksek okulu, Ağaçişleri Endüstri Mühendisliği Bölümü, Yayın No: 29, Ankara.
7. İLTER, H.K. 1998: İşletme Fonksiyonlarının Optimizasyonunda Çok Yönlü Kuyruk Modelleri ve Bir Uygulama, G.Ü. Sosyal Bilimler Enstitüsü, Yüksek Lisans Tezi, Ankara.